21.01.2021
Геометрія
Тема. Відстань від прямої до площини.
https://youtu.be/CMxTWikJcU8
Домашнє завдання
Параграф 2 (стор.306 - 307), номер 9.8; 9.14.
20.01.2021
Алгебра
Тема .Формули зведення. Самостійна робота
19.01.2021
Геометрія
Тема. Відстань від точки до прямої і площини.
https://youtu.be/i3OMhWF8yAo
https://youtu.be/zsKcjytMKww
Домашня робота: параграф 9 ст. (305 - 307), номер 9.4 (1-4).
15.01.2021
АЛГЕБРА
Тема. Формули зведення
Відео: https://www.youtube.com/watch?v=j0_occ6S9no
Прочитайте приклади, які розв'язані у підручнику ( сторінка 102 - 105).
Домашня робота
Параграф 11, номер 11.4; 11.8 (5,6); 11.20 (2).
14.01.2021
ГЕОМЕТРІЯ
Тема. Перпендикулярність площин
Презентація: https://naurok.com.ua/prezentaciya-do-uroku-z-geometri-dlya-10-klasu-riven-standart-na-temu-perpendikulyarnist-ploschin-95174.html
Домашня робота
Параграф 8, ст. 299 - 300, № 8.12; 8.14.
13.01. 2021
АЛГЕБРА
Тема. Основні співвідношення між тригонометричними функціями одного аргументу
Презентація: https://naurok.com.ua/prezentaciya-osnovni-spivvidnoshennya-mizh-trigonometrichnimi-funkciyami-odnogo-y-togo-samogo-argumentu-115148.html
Параграф 10 , № 10.23 (4,6); 10.28 (2).
12.01.2021
ГЕОМЕТРІЯ
Тема. Двогранний кут.
Читаємо пункт 1, сторінка 298-299. Розберіть задачу 1 з підручника.
Відео: https://www.youtube.com/watch?v=BV0XKEstQBQ
Домашня робота. № 8.7; 8.10.
19.05.2020 ГЕОМЕТРІЯ
18.05.2020 АЛГЕБРА
14.05.2020 АЛГЕБРА
12.05.2020 ГЕОМЕТРІЯ
Підсумкова контрольна робота з геометрії
https://naurok.com.ua/pidsumkova-kontrolna-robota-z-geometri-10-klas-176341.html18.05.2020 АЛГЕБРА
14.05.2020 АЛГЕБРА
12.05.2020 ГЕОМЕТРІЯ
Розв'язування задач з теми "Вектори та дії над ними!
https://naurok.com.ua/rozv-yazuvannya-zadach-z-temi-vektori-ta-di-nad-koordinatami-vektoriv-18412.html
07.05.2020 АЛГЕБРА
ТЕМА ПОВТОРЕННЯ: Функції їх властивості та графіки.
https://www.youtube.com/watch?v=hHtgl-pLyUk
05.05.2020 ГЕОМЕТРІЯ
ТЕМА ПОВТОРЕННЯ: КООРДИНАТИ І ВЕКТОРИ!
15.04.2020 ГЕОМЕТРІЯ
КОНТРОЛЬНА РОБОТА https://naurok.com.ua/urok-kontrolna-robota-z-temi-koordinati-ta-vektori-v-prostori-33787.html
13.04.2020 АЛГЕБРА
09.04.2020 АЛГЕБРА
07.04.2020 ГЕОМЕТРІЯ
06.04.2020 АЛГЕБРА
03.04.2020 ГЕОМЕТРІЯ
РОЗВЯЗУВАННЯ ЗАДАЧ


02.04.2020 АЛГЕБРА
САМОСТІЙНА РОРБОТА
https://naurok.com.ua/samostiyna-robota-dlya-10-klasu-z-temi-koordinati-i-vektori-u-prostori-9505.html
30.03.2020 АЛГЕБРА 10 КЛАС
27.03.2020 ГЕОМЕТРІЯ 10 КЛАС
ПЕРЕХОДИМО ПО ССИЛЦІ:https://naurok.com.ua/kut-mizh-vektorami-skalyarniy-dobutok-vektoriv-148369.html
Тема уроку. Кут між векторами. Скалярний добуток векторів.
Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв'язування задач.
Обладнання: схема "Вектори в просторі»
Хід уроку
І. Перевірка домашнього завдання
1. Фронтальна бесіда з класом за контрольними запитаннями № 18— 20 з використанням схеми «Вектори в просторі» (див. с. 233).
2. Відповіді на запитання, які виникли в учнів при розв'язуванні за¬дач № 51-53.
3. Математичний диктант.
Дано вектори:
Варіант 1 — (3; 0; 4); (7; 0; 2); Варіант 2 — (2; -2; 0); (3; 0; -3).
Запишіть:
1) координати вектора , якщо = + , (2 бали)
2) координати вектора , якщо = 2 - ; (2 бали)
3) довжину вектора + ; (2 бали)
4) координати вектора , якщо відомо, що довжина вектора втри¬чі більша довжини вектора ; (2 бали)
5) при якому значенні k вектор (k; 0; 6) колінеарний вектору ; (2 бали)
6) чи компланарні вектори , та (0; 0; 1)? (2 бали)
Відповідь. Варіант 1. 1) (10; 0; 6). 2) (-1; 0; 6). 3) 2 .
4) (-9; 0; -12), (9; 0; 12). 5) k = 21. 6) Так.
Варіант 2. 1) (5; -2; -3). 2) (1; -4; 3). 3) .
4) (6; -6; 0), (-6; 6; 0). 5) k = - 6. 6) Hi.
II. Сприйняття й усвідомлення нового матеріалу
Скалярний добуток векторів
Скалярним добутком векторів (аx; аy; аz) ∙ (bx; by; bz) назива¬ється число (скаляр) • = аx • bx + аy • by + аz • bz.
Розв'язування задач
1. Знайдіть • , якщо (-2; 3; 1), (-4; -5; 2).
2. Дано вектори (2; -1; 4), (5; 3; n). При якому значенні п скаляр¬ний добуток векторів дорівнює -3?
Із означення скалярного добутку двох векторів і випливають його властивості.
1) • = • .
2) ( + ) • = • + • .
3) Скалярний добуток векторів і дорівнює добутку їх абсолютних величин на косинус кута між ними: • = • cos φ (рис. 297).
Доведення
Від точки О відкладемо вектор OВ = (рис. 298) і ОА = . Виберемо декартову систему координат так, щоб точка О була початком коорди¬нат, пряма ОА збіглася з віссю у, вісь z була б перпендикулярна до пря¬мої ОА і знаходилася в площині ОАВ, вісь х перпендикулярна до площи¬ни уz. Визначимо координати векторів і :
А(0; | | ; 0); B(0; | | cos φ; | | sin φ); (0; | |; 0); (0; | | cos φ; | | sin φ).
Знайдемо скалярний добуток:
• = 0 • 0 + | | • | | cos φ + 0 • | | sin φ = | | • | | cos φ.
Наслідки із властивості 3:
1)
2) Два відмінні від нуля вектори і перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
Дійсно, якщо • = 0, то • • cos φ = 0 , cos φ = 0, φ = , і навпаки, якщо φ = 0 , то • = • • cos φ = • • 0 = 0.
Розв'язування задач
1. Знайдіть • , якщо = 5, = 4, а кут між векторами дорів¬нює 120°.
2. Ребро куба дорівнює 4 (рис. 299). Знайдіть • .
3. Чи перпендикулярні вектори (2; 3; 6) і (3; 2; -1)?
4. При якому значенні т вектори (6; 0; 12) і (-8; 13; m) перпенди-кулярні?
5. Чи є серед векторів (2; 3; 1), (5; 9; 2), (-3, 1; 3) ортогональні вектори?
6. Який кут утворюють вектори (-5; 0; 0) і (0; 3; 0)?
7. Знайдіть кут між векторами (1; 1; 0) і (1; 0; 1).
8. Знайдіть cos ABC, якщо А(1; -3; 4), В(2; -2; 6), С(3; 1; 3).
III. Домашнє завдання
§ 4, п. 35, 36; контрольні запитання № 18—20; задачі № 55 (1; 4), 56 (с. 58).
IV. Підведення підсумку уроку
Запитання до класу
1) Що називається скалярним добутком векторів (аx; аy; аz) і (bx; by; bz)?
2) Сформулюйте властивості скалярного добутку векторів.
3) Яка умова ортогональності двох ненульових векторів?
4) У просторі дано вектори (1; 1; -1), (0; -1; 1). Укажіть, які з вказаних тверджень правильні, а які — неправильні:
а) = 1;
б) вектори і перпендикулярні;
в) вектори + і не перпендикулярні;
г) •( + ) = 1;
д) вектори і + утворюють кут, косинус якого дорівнює .
26.03.2020 р.Біологія 10 клас.
Тема Сучасні завдання медичної генетики.
Підручник п. 51.
Презентація до теми https://naurok.com.ua/prezentaciya-zavdannya-suchasno-medichno-genetiki-114040.html.
Відео до теми https://www.youtube.com/watch?v=Y-N1PEPJrT0
УРОК АЛГЕБРА 10 КЛАС
ТЕМА: Ознаки сталості функції
ПРОШУ ПЕРЕХОДИТИ ПО ССИЛЦІ:
https://naurok.com.ua/prezentaciya-do-uroku-z-algebri-v-11kl-ekstremumi-funkci-neobhidna-i-dostatnya-umova-ekstremumu-11727.html
07.05.2020 АЛГЕБРА
ТЕМА ПОВТОРЕННЯ: Функції їх властивості та графіки.
https://www.youtube.com/watch?v=hHtgl-pLyUk
05.05.2020 ГЕОМЕТРІЯ
ТЕМА ПОВТОРЕННЯ: КООРДИНАТИ І ВЕКТОРИ!
15.04.2020 ГЕОМЕТРІЯ
КОНТРОЛЬНА РОБОТА https://naurok.com.ua/urok-kontrolna-robota-z-temi-koordinati-ta-vektori-v-prostori-33787.html
13.04.2020 АЛГЕБРА
09.04.2020 АЛГЕБРА
07.04.2020 ГЕОМЕТРІЯ
Самостійна робота
Варіант 1
1) Задано точки A(2;-1;3) і В(-4;1;3).
а) Знайдіть довжину відрізка AB.
б) Опишіть розташування в прямокутній системі координат середини відрізка AB.
в) Знайдіть координати вектора 
2) Доведіть, що вектори  перпендикулярні, якщо A(2;1;-8), B(1;-5;0), C (8;1;-4), D(9;7;-12).
перпендикулярні, якщо A(2;1;-8), B(1;-5;0), C (8;1;-4), D(9;7;-12).
Варіант 2
1) Задано точки A (-2;1;-3) і B(2;1;3).
а) Знайдіть довжину відрізка AB.
б) Опишіть розташування в прямокутній системі координат середини відрізка AB.
в) Знайдіть координати вектора 
2) Доведіть, що вектори  перпендикулярні, якщо A(6;7;8), B(8;2;6), C(4;3;2), D(2;8;4).
перпендикулярні, якщо A(6;7;8), B(8;2;6), C(4;3;2), D(2;8;4).
03.04.2020 ГЕОМЕТРІЯ
РОЗВЯЗУВАННЯ ЗАДАЧ
Виконання тестових завдань із подальшою самоперевіркою і самооцінюванням
Варіант 1
1) Чому дорівнює скалярний добуток векторів 
А. 6. Б. 22. В. 16. Г. -6.
2) Задано вектори  При якому значенні x
При якому значенні x 
А. 3. Б. 0. В. 7/4. Г. -3.
3) Чому дорівнює кут між векторами 
А. 0°. Б. 60°. В. 90°. Г. 120°.
Варіант 2
1) Чому дорівнює скалярний добуток векторів 
А. 1. Б. -11. В. 11. Г. -7.
2) Задано вектори  При якому значенні у
При якому значенні у 
А. 5. Б. 4. В. 0. Г. 5/2.
3) Чому дорівнює кут між векторами 
А. 0°. Б. 60°. В. 90°. Г. 120°.
Виконання завдань на встановлення відповідності
Установіть відповідність між вектором (1-4) і перпендикулярним йому вектором (А-Д).

1) Довжина ребра куба ABCDA1B1C1D1 дорівнює 2. Обчисліть скалярний добуток векторів:
2) Знайдіть зовнішній кут при вершині A трикутника ABC, якщо A (1;3;0), B(1;0;4), C(-2;1;6).
3) Точки A(1;1;5), B(4;7;5), C(8;5;5), D(5;-1;5) є вершинами прямокутника ABCD. Знайдіть більший кут між діагоналями прямокутника.
02.04.2020 АЛГЕБРА
САМОСТІЙНА РОБОТА
| В - 1 | 7 балів | В - ll | |
| 1. Знайти проміжки, на яких функція зростає, спадає. | |||
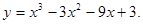 | 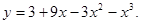 | ||
| 2. Знайти критичні точки функції. | |||
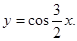 | 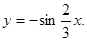 | ||
| В – lll | 9 балів | В – lV | |
| 1. Знайти проміжки, на яких функція зростає, спадає. | |||
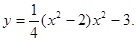 | 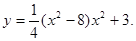 | ||
| 2. Знайти критичні точки функції. | |||
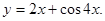 | 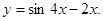 | ||
| В – V | 12 балів | В – Vl | |
| 1. Знайти проміжки, на яких функція зростає, падає. | |||
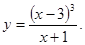 | 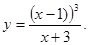 | ||
| 2. Знайти критичні точки функції. | |||
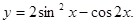 | 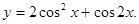 | ||
Контрольна робота
31.03.2020 ГЕОМЕТРІЯ 10 КЛАССАМОСТІЙНА РОРБОТА
https://naurok.com.ua/samostiyna-robota-dlya-10-klasu-z-temi-koordinati-i-vektori-u-prostori-9505.html
30.03.2020 АЛГЕБРА 10 КЛАС
ТОЧКИ ЕКСТРЕМУМУ ФУНКЦІЇ
27.03.2020 ГЕОМЕТРІЯ 10 КЛАС
ПЕРЕХОДИМО ПО ССИЛЦІ:https://naurok.com.ua/kut-mizh-vektorami-skalyarniy-dobutok-vektoriv-148369.html
Тема уроку. Кут між векторами. Скалярний добуток векторів.
Мета уроку: формування понять кута між векторами, скалярного добутку векторів. Формування вмінь учнів застосовувати вивчений матеріал до розв'язування задач.
Обладнання: схема "Вектори в просторі»
Хід уроку
І. Перевірка домашнього завдання
1. Фронтальна бесіда з класом за контрольними запитаннями № 18— 20 з використанням схеми «Вектори в просторі» (див. с. 233).
2. Відповіді на запитання, які виникли в учнів при розв'язуванні за¬дач № 51-53.
3. Математичний диктант.
Дано вектори:
Варіант 1 — (3; 0; 4); (7; 0; 2); Варіант 2 — (2; -2; 0); (3; 0; -3).
Запишіть:
1) координати вектора , якщо = + , (2 бали)
2) координати вектора , якщо = 2 - ; (2 бали)
3) довжину вектора + ; (2 бали)
4) координати вектора , якщо відомо, що довжина вектора втри¬чі більша довжини вектора ; (2 бали)
5) при якому значенні k вектор (k; 0; 6) колінеарний вектору ; (2 бали)
6) чи компланарні вектори , та (0; 0; 1)? (2 бали)
Відповідь. Варіант 1. 1) (10; 0; 6). 2) (-1; 0; 6). 3) 2 .
4) (-9; 0; -12), (9; 0; 12). 5) k = 21. 6) Так.
Варіант 2. 1) (5; -2; -3). 2) (1; -4; 3). 3) .
4) (6; -6; 0), (-6; 6; 0). 5) k = - 6. 6) Hi.
II. Сприйняття й усвідомлення нового матеріалу
Скалярний добуток векторів
Скалярним добутком векторів (аx; аy; аz) ∙ (bx; by; bz) назива¬ється число (скаляр) • = аx • bx + аy • by + аz • bz.
Розв'язування задач
1. Знайдіть • , якщо (-2; 3; 1), (-4; -5; 2).
2. Дано вектори (2; -1; 4), (5; 3; n). При якому значенні п скаляр¬ний добуток векторів дорівнює -3?
Із означення скалярного добутку двох векторів і випливають його властивості.
1) • = • .
2) ( + ) • = • + • .
3) Скалярний добуток векторів і дорівнює добутку їх абсолютних величин на косинус кута між ними: • = • cos φ (рис. 297).
Доведення
Від точки О відкладемо вектор OВ = (рис. 298) і ОА = . Виберемо декартову систему координат так, щоб точка О була початком коорди¬нат, пряма ОА збіглася з віссю у, вісь z була б перпендикулярна до пря¬мої ОА і знаходилася в площині ОАВ, вісь х перпендикулярна до площи¬ни уz. Визначимо координати векторів і :
А(0; | | ; 0); B(0; | | cos φ; | | sin φ); (0; | |; 0); (0; | | cos φ; | | sin φ).
Знайдемо скалярний добуток:
• = 0 • 0 + | | • | | cos φ + 0 • | | sin φ = | | • | | cos φ.
Наслідки із властивості 3:
1)
2) Два відмінні від нуля вектори і перпендикулярні тоді і тільки тоді, коли їх скалярний добуток дорівнює нулю.
Дійсно, якщо • = 0, то • • cos φ = 0 , cos φ = 0, φ = , і навпаки, якщо φ = 0 , то • = • • cos φ = • • 0 = 0.
Розв'язування задач
1. Знайдіть • , якщо = 5, = 4, а кут між векторами дорів¬нює 120°.
2. Ребро куба дорівнює 4 (рис. 299). Знайдіть • .
3. Чи перпендикулярні вектори (2; 3; 6) і (3; 2; -1)?
4. При якому значенні т вектори (6; 0; 12) і (-8; 13; m) перпенди-кулярні?
5. Чи є серед векторів (2; 3; 1), (5; 9; 2), (-3, 1; 3) ортогональні вектори?
6. Який кут утворюють вектори (-5; 0; 0) і (0; 3; 0)?
7. Знайдіть кут між векторами (1; 1; 0) і (1; 0; 1).
8. Знайдіть cos ABC, якщо А(1; -3; 4), В(2; -2; 6), С(3; 1; 3).
III. Домашнє завдання
§ 4, п. 35, 36; контрольні запитання № 18—20; задачі № 55 (1; 4), 56 (с. 58).
IV. Підведення підсумку уроку
Запитання до класу
1) Що називається скалярним добутком векторів (аx; аy; аz) і (bx; by; bz)?
2) Сформулюйте властивості скалярного добутку векторів.
3) Яка умова ортогональності двох ненульових векторів?
4) У просторі дано вектори (1; 1; -1), (0; -1; 1). Укажіть, які з вказаних тверджень правильні, а які — неправильні:
а) = 1;
б) вектори і перпендикулярні;
в) вектори + і не перпендикулярні;
г) •( + ) = 1;
д) вектори і + утворюють кут, косинус якого дорівнює .
Тема Сучасні завдання медичної генетики.
Підручник п. 51.
Презентація до теми https://naurok.com.ua/prezentaciya-zavdannya-suchasno-medichno-genetiki-114040.html.
Відео до теми https://www.youtube.com/watch?v=Y-N1PEPJrT0
Домашня робота
Опрацювати параграф 51
2. Виконати проект (одна тема на вибір):
- Генетичний моніторинг в людських спільнотах.
- Скринінг-програми для новонароджених.
- Генотерапія та її перспективи.
3. З метою підготовки до ЗНО та закріплення знань з теми «Спадковість та мінливість» пройти тестування на Тесторіумі
ТЕМА: Ознаки сталості функції
ПРОШУ ПЕРЕХОДИТИ ПО ССИЛЦІ:
https://naurok.com.ua/prezentaciya-do-uroku-z-algebri-v-11kl-ekstremumi-funkci-neobhidna-i-dostatnya-umova-ekstremumu-11727.html










































Комментариев нет:
Отправить комментарий